TEK 2/2025 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen ja Topi Törmä, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen
Voit pelata Divisium-3-pelejä myös verkkosivuillamme!
Alta löydät Sudokun ja Divisium-3:n ratkaisut. Pulmien ratkaisut julkaisemme tällä sivulla 28.4. kun vastausaika Pulmakulman 2/25 lukijakilpailuun on päättynyt.
SUDOKU

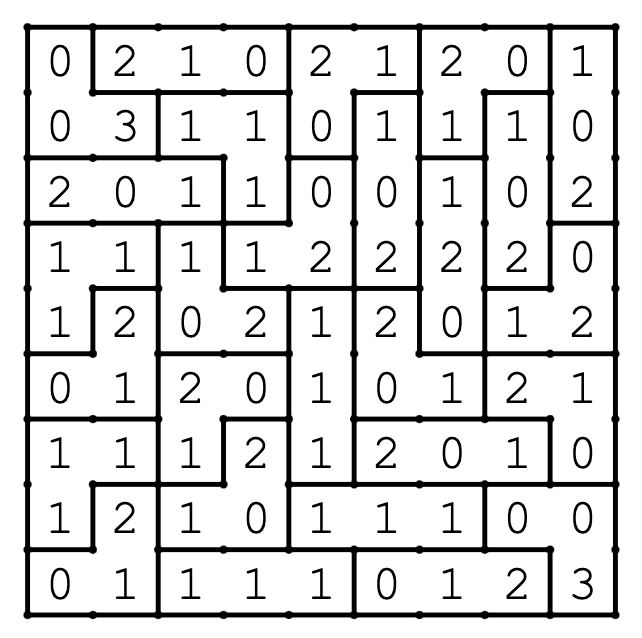
DIVISIUM-3
TEK 1/2025 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen ja Topi Törmä, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen
Saimme 14 vastausta TEK-lehden 1/25 Pulmakulmaan. Kiitos kaikille ratkaisut lähettäneille! Palkinnon voitti Mikko Malmi Espoosta.
Voit pelata Divisium-3-pelejä myös verkkosivuillamme!
PULMA 1
Ongelma: Lisää alla olevien numeroiden väliin ja ympärille sulkeita sekä yhteen-, vähennys, kerto- ja/tai jakolaskumerkkejä niin, että lausekkeen arvo on 2025.

Ratkaisu: Esimerkiksi
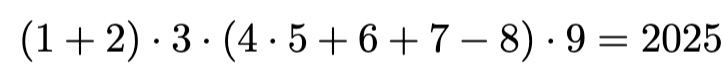
PULMA 2
Ongelma: Suorakulmion sivujen pituudet ovat positiiviset kokonaisluvut a ja b, missä a on korkeintaan b. Mitkä ovat lukujen a ja b mahdolliset arvot, kun suorakulmion piiri ja pinta-ala ovat yhtä suuret?
Ratkaisu: Suorakulmion piiri on 2a+2b ja pinta-ala ab. Saadaan siis yhtälö 2a+2b=ab, josta saadaan yhtäpitävästi ab-2a-2b+4=4 eli (a-2)(b-2)=4. Koska a ja b ovat kokonaislukuja, niin yhtälön ainoat ratkaisut ovat a-2=1 ja b-2=4 sekä a-2=2 ja b-2=2. Siispä a=3 ja b=6 tai a=b=4.
PULMA 3
Ongelma: 250 pelikorttia, joiden arvot ovat 1–250 asetetaan riviin satunnaisessa järjestyksessä. Kaksi pelaajaa pelaa peliä, jossa omalla vuorollaan saa ottaa yhden kortin rivin jommasta kummasta päästä. Kun kaikki kortit on otettu, korttien arvot lasketaan yhteen, ja pelin voittaa se, jonka korttien yhteenlaskettu arvo on suurempi. Kummalla pelaajalla on pelissä voittava strategia ja mikä se on? Voiko peli päättyä tasapeliin?
Ratkaisu: Koska kaikkien korttien yhteenlaskettu arvo 1+2+...+250= 31 375 on pariton luku, niin peli ei voi päättyä tasapeliin.
Ensimmäisellä pelaajalla on seuraavanlainen voittava strategia: Kuvitellaan, että rivissä joka toinen kortti on väriltään sininen ja joka toinen on punainen. Ensimmäinen pelaaja voi laskea, kumman väristen korttien arvojen summa on suurempi. Koska kortteja on parillinen määrä, niin alussa rivin päissä on eriväriset kortit. Näin ollen ensimmäinen pelaaja voi valita suuremman summan tuottavan värisen kortin. Tämän jälkeen toinen pelaaja joutuu ottamaan pienemmän summan tuottavan värisen kortin. Ensimmäinen pelaaja jatkaa pelin loppuun keräämällä samanvärisiä kortteja ja näin voittaa pelin.
PULMA 4
Ongelma: Mitkä positiiviset kokonaisluvut voi esittää vähintään kahden peräkkäisen positiivisen kokonaisluvun summana? Esimerkiksi luvun 14 voi esittää näin, sillä 14=2+3+4+5.
Ratkaisu: Osoitetaan, että kaikki muut positiiviset kokonaisluvut voi esittää vähintään kahden peräkkäisen positiivisen kokonaisluvun summana paitsi luvun 2 potenssit (mukaan lukien 1 eli 2 potenssiin nolla).
Aritmeettisen summan kaavan nojalla k peräkkäisen positiivisen kokonaisluvun summa on
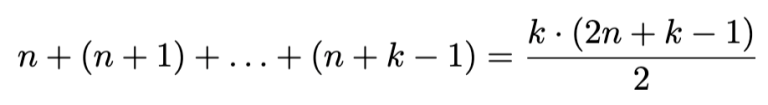
jollakin positiivisella kokonaisluvulla n. Yllä olevalla summalla on väistämättä pariton tekijä, sillä luvuista k ja 2n+k-1 toinen on parillinen ja toinen pariton. Näin ollen summa ei voi olla kakkosen potenssi. Osoitetaan vielä, että muut kokonaislukuarvot ovat mahdollisia.
Jos kokonaisluku on parillinen, mutta ei kakkosen potenssi, niin se on muotoa
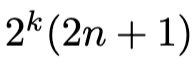
, joillakin positiivisilla kokonaisluvuilla n ja k. Jos
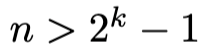
, niin
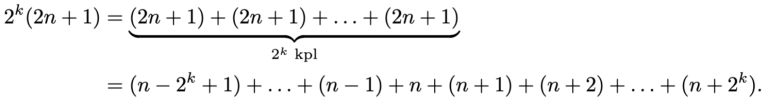
Jos taas
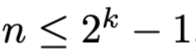
, niin
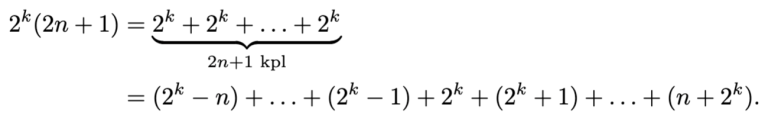
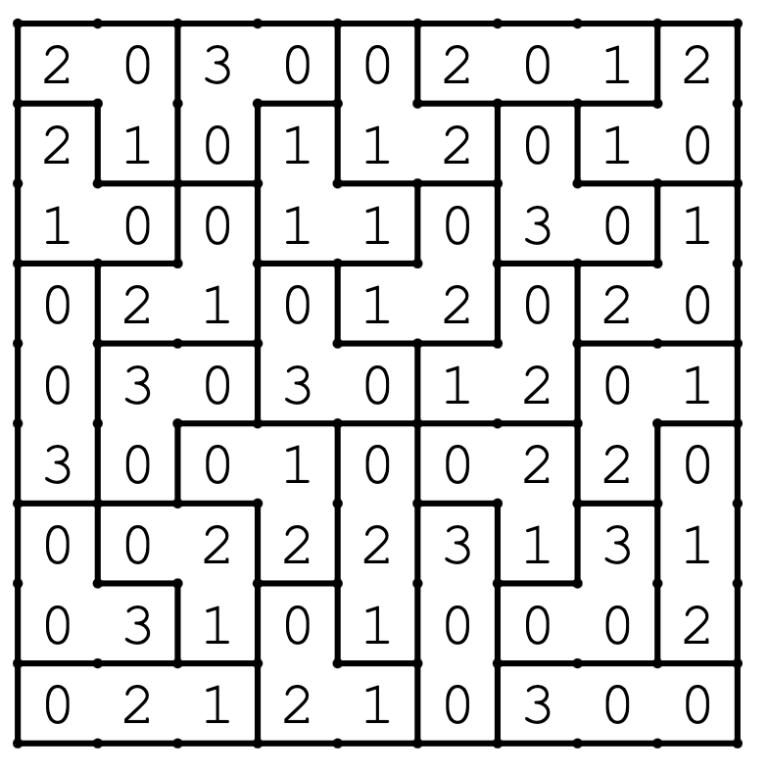
SUDOKU

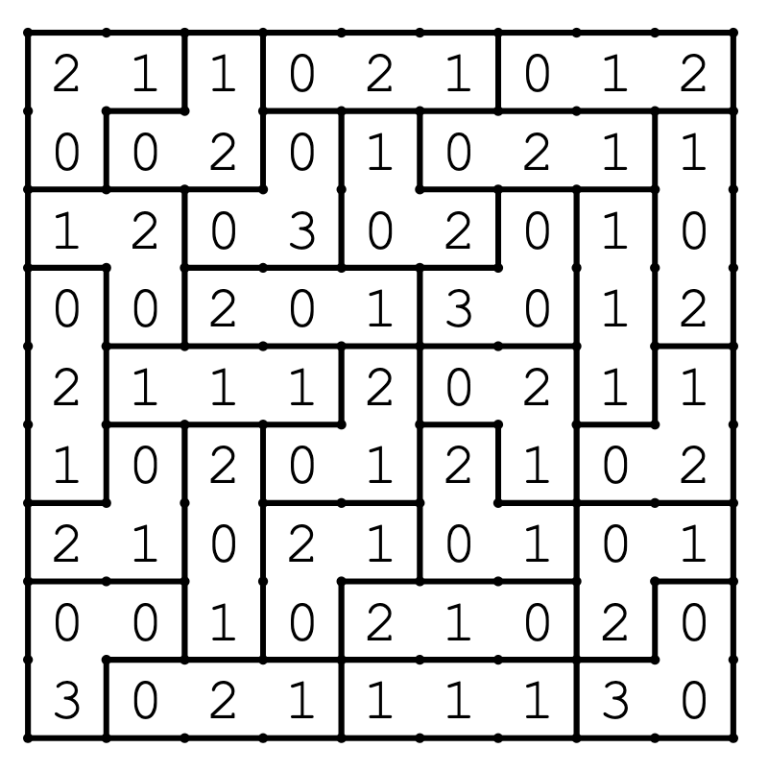
DIVISIUM-3
TEK 5/2024 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen ja Topi Törmä, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen
PULMA 1
Ongelma: Oletetaan, että auton rekisterikilvessä on 3 kirjainta 26 kirjaimen aakkostosta. Kuinka monta mahdollisuutta on, jos kirjaimet ovat aakkosjärjestyksessä? (Huom. esimerkiksi AAB kelpaa.)
Ratkaisu: Jos kaikki kirjaimet ovat sama, niin vaihtoehtoja on 26 kappaletta. Jos kaikki kirjaimet ovat eri, niin vaihtoehtoja on niin monta kuin miten monella tavalla 3 kirjainta voidaan valita 26 kirjaimesta, eli 26 yli 3 vaihtoehtoa. Jos taas kirjaimista tasan kaksi on samoja, niin eri kirjaimet voidaan valita 26 yli kahden eri tavalla ja lisäksi kahdella tavalla se, mikä kirjain on kahdesti. Yhteensä saadaan siis
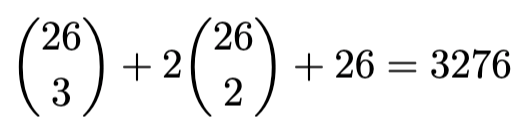
vaihtoehtoa.
PULMA 2
Ongelma: Onko luku
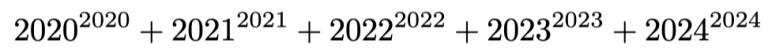
jaollinen luvulla 10?
Ratkaisu: Ei ole. Jotta luku olisi jaollinen kymmenellä, tulisi sen olla sekä viidellä että kahdella jaollinen. Luku on jaollinen kahdella. Osoitetaan seuraavaksi, että se ei ole jaollinen viidellä. Ensimmäinen summattava on jaollinen viidellä. Koska 2021 antaa jakojäännöksen 1 jaettaessa viidellä, antavat myös kaikki sen potenssit jakojäännöksen 1 jaettaessa viidellä. Luku 2022 antaa jakojäännöksen 2 jaettaessa viidellä. Sen potenssit muodostavat jakojäännösjonon 2, 4, 3, 1, 2, 4, 3, 1,... jaettaessa viidellä. Jos eksponenttina on 2022, on jakojäännös siis 4. Luku 2023 antaa jakojäännöksen 3 jaettaessa viidellä. Sen potenssit muodostavat jakojäännösjonon 3, 4, 2, 1, 3, 4, 2, 1,... jaettaessa viidellä. Jos eksponenttina on 2023, on jakojäännös siis 2. Luvun 2024 jakojäännös viidellä jaettaessa on 4. Sen potenssit muodostavat jonon 4, 1, 4, 1,... Jos eksponentti on 2024, on jakojäännös siis 1. Koko summan jakojäännös viidellä jaettaessa on siis 1+4+2+1=8, eli 3. Summa ei ole jaollinen kymmenellä.
Huom. Tehtävä olisi ratkaistavissa nätisti kongruensseilla, mutta ratkaisu kirjoitettiin niin, että lukijan ei tarvitse olla kuullut kongruensseista.
PULMA 3
Ongelma: 50 oppilaan luokassa jokainen lähetti 25 joulukorttia muille luokan oppilaille. Osoita, että ainakin jotkut kaksi oppilasta saivat kumpikin kortin toisiltaan.
Lähde: Kreikka, kansallinen kilpailu 2007
Ratkaisu: Kahden oppilaan pareja on
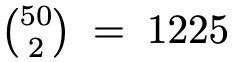
Jos ketkään kaksi eivät lähetä toisilleen, antaa tämä ylärajan joulukorttien määärälle. Toisaalta tiedetään, että joulukortteja lähetetään
eli enemmän. Ei siis ole mahdollista, että ketkään kaksi eivät olisi lähettäneet toisilleen joulukortteja.
PULMA 4
Ongelma: Suorakulmaisen kolmion kateettien a ja b summa on 24. Hypotenuusan vastaisen korkeusjanan pituus on 7. Määritä hypotenuusan pituus.
Lähde: Norja, kansallinen kilpailu 2003
Ratkaisu: Merkitään hypotenuusan pituutta kirjaimella c. Kolmion ala voidaan laskea kahdella eri tavalla. Saadaan yhtälö 7c = ab. Lisäksi a+b = 24. Pythagoraan lauseen perusteella saadaan
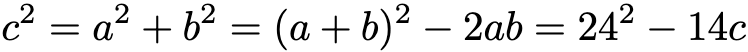
Tämä on toisen asteen yhtälö, jonka ratkaisut ovat c = 18 ja c = -32. Ainoastaan positiivinen ratkaisu on mahdollinen, joten hypotenuusan pituus on 18.
SUDOKU

DIVISIUM-3
TEK 4/2024 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen
PULMA 1
Ongelma: Määritä ne kaikki kokonaisluvut k, jotka voidaan esittää muodossa k = a² + b² - c² - d², missä a, b, c ja d ovat kokonaislukuja.
Ratkaisu: Ratkaisu päivitetty oikeaksi 30.9.2024 kello 14.10. Osoitetaan, että kaikki kokonaisluvut voidaan esittää tässä muodossa. Jos jokin positiivinen kokonaisluku n voidaan esittää tässä muodossa, niin tällöin luku -n voidaan esittää vaihtamalla lukujen a ja c ja b ja d paikat. Lisäksi 0 voidaan esittää valitsemalla a = b = c = d.
Koska kahden peräkkäisen neliön erotukset antavat kaikki parittomat luvut, saadaan pariton positiivinen luku 2n + 1 esitettyä valitsemalla a = n + 1, b = 0, c = n ja d = 0. Parillinen positiivinen kokonaisluku 4n+2 saadaan esitettyä valitsemalla a = b = n + 1 ja c = d = n ja parillinen positiivinen kokonaisluku 4n+4 puolestaan valinnoilla a=n+2, c=n ja b=d=0.
PULMA 2
Ongelma: Neliön ABCD keskipisteen M heijastuma pisteen C yli on E. Sen ympyrän, joka kulkee kolmion BDE kaikkien kärkien kautta ja suoran AM leikkauspiste on S. Osoita, että S on janan AM keskipiste. (Lähde: Itävalta, 2008)
Ratkaisu: Tehtävän voi ratkaista kehäkulmalauseen avulla tai analyyttisella geometrialla. Esitetään tässä ratkaisu pisteen potenssin avulla. Koska M on neliön keskipiste, niin |ME| = 2|MB| = 2|MD| = 2|MA|. Pisteen potenssin perusteella |ME||MS| = |MB||MD|. Siispä
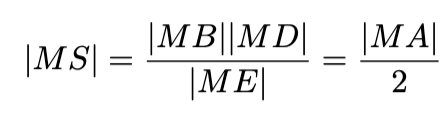
Väite on todistettu.
PULMA 3
Ongelma: Kahvikuppi on katkaistun kartion muotoinen. Sen pohjan halkaisija on 8 cm ja ylhäältä sen halkaisija on 10 cm. Kupin korkeus on myös 10 cm. Kuinka korkealle kuppi pitää täyttää, että se on täsmälleen puolillaan?
Ratkaisu: Ratkaisu päivitetty oikeaksi 27.9.2024 kello 10.10. Ratkaistaan yksinkertaisuuden vuoksi katkaistun kartion tilavuuden kaavalla. Yksikkönä on senttimetri, mutta jätetään yksiköt pois lausekkeista. Kahvikupin kokonaistilavuus on

Jos kahvia kaadetaan korkeudelle h, niin kupin säde kahvin huippukorkeudella on h / 10 + 4. Tällöin kahvin tilavuus on
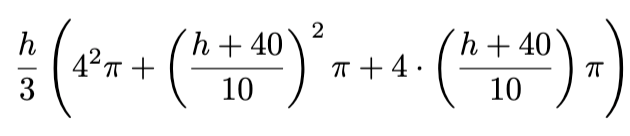
Riittää siis ratkaista yhtälö
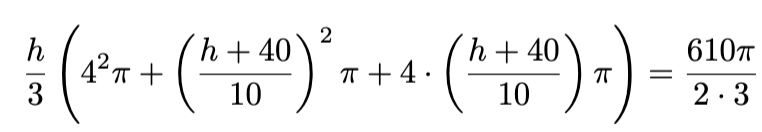
Saadaan kahvin korkeudeksi n. 5,5 cm.
PULMA 4
Ongelma: Määritä kaikki positiiviset kokonaislukuparit (m, n), jotka toteuttavat ehdot: m jakaa luvun 2n - 1 ja n jakaa luvun 2m - 1. (Lähde: Kroatian kansallisen kilpailun finaali 2011, t. 2.1 ja Tsekkiläis-slovakialaisten matematiikkaolympialaisten toinen kierros 2010, t. 3)
Ratkaisu: Oletetaan aluksi, että m = n tai m < n. On oltava
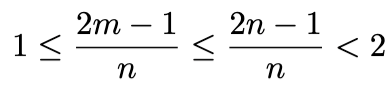
Siispä 2m - 1 = n. Saadaan 2n - 1 = 4m - 3, ja koska tämän on oltava jaollinen luvulla m, on oltava m = 1 tai m = 3. Kumpikin vaihtoehto on mahdollinen. Saadaan parit (1,1) ja (3,5). Jos taas m > n, niin vastaavasti saadaan pari (5,3).
SUDOKU

DIVISIUM-3
Vanhojen Pulma-tehtävien lähteitä
TEK 3/2024 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut sekä Pakopulmien mallivastaukset
Tehtävät: Anne-Maria Ernvall-Hytönen ja Esa Vesalainen, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen, Pakopulmat: Veli-Matti Saarinen
PULMA 1
Ongelma: Olkoon n kokonaisluku, joka on vähintään 4. Piirrämme yksikköympyrän sisälle n yhtenevää yksikköympyrän kaarta kuten oheisessa kuvassa, jossa on kuvattu tapaus n = 7. Mikä onkaan tummennetun alueen ala?
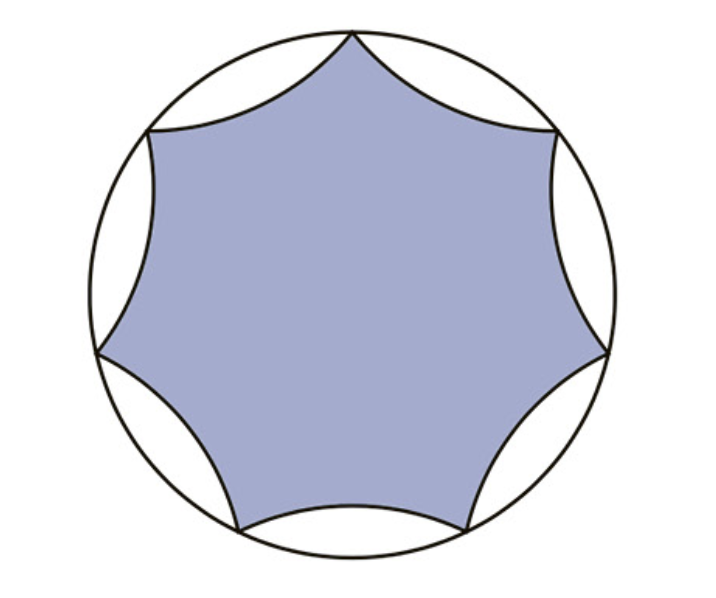
Ratkaisu: Yhden kaaren keskuskulma on 360/n astetta, joten yhden segmentin ala on
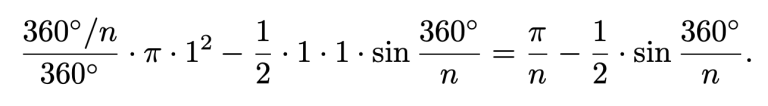
Eli kysytty ala on
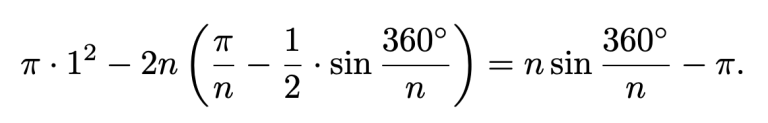
PULMA 2
Ongelma: Suorakulmion sivujen pituudet ja pinta-ala ovat erään aritmeettisen jonon kolme peräkkäistä jäsentä. Lisäksi ne ovat kokonaislukuja. Määritä mahdolliset sivujen pituudet ja ala.
Ratkaisu: Jos jokin sivu on pituudeltaan nolla, on myös suorakulmion ala nolla, jolloin myös toinen sivu on nolla.
Oletetaan nyt, että sivujen pituudet ovat positiivisia (sillä ne eivät voi olla negatiivisia). Jos sivut ovat a ja b, niin tulo ab on vähintään yhtä suuri kuin max{a,b}.
Jos siis jono on h-d, h, h+d, niin h+d on ala. Tulee siis olla h(h-d) = h+d. Koska kaikki luvut ovat kokonaislukuja, niin h jakaa luvun d. Kirjoitetaan d = ah ja sijoitetaan lausekkeeseen h(h-ah) = h+ah, joten h-ah = 1+a, eli h-ah-a-1 = (h+1)(1-a) = 2. Koska h on suorakulmion sivu, sen täytyy olla positiivinen. Siispä h+1 on vähintään 2, joten h+1 = 2 ja 1-a = 1. Saadaan h=1 ja a=0. Saadaan ainoaksi mahdollisuudeksi yksikköneliö.
PULMA 3
Ongelma: Lindalla on rakennuspalikoita ja kolme laatikkoa, joissa säilyttää niitä. Ensimmäiseen hän laittaa kolme seitsemäsosaa palikoistaan, toiseen jonkin positiivisen määrän viidesosia jäljellä olevista palikoista, ja kolmanteen loput 572 palikkaa. Kuinka monta palikkaa hänellä on yhteensä?
Ratkaisu: Olkoon hänen palikoidensa kokonaismäärä N. Ensimmäiseen laatikkoon hän siis laittaa 3N/7 palikkaa. Toiseen laatikkoon hän laittaa 4N/7·k/5 palikkaa, missä k on jokin luvuista 1, 2, 3 ja 4. Lopuksi, kolmanteen laatikkoon päätyvät loput 4N/7·(5–k)/5 = 572 palikkaa. Koska 572 on lukujen 4, 11 ja 13 tulo, on N·(5–k) = 5·7·11·13. Erotus 5-k on jokin luvuista 1, 2, 3 ja 4, ja oikean puolen tekijä. Tämä on mahdollista vain ja ainoastaan, jos 5-k = 1, eli k=4, joten N = 5·7·11·13 = 5 005.
PULMA 4
Ongelma: Meillä on 2 024 punnusta, joiden painot ovat 2 024 pienintä positiivista Fibonaccin lukua
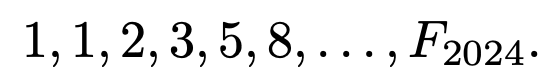
Jokainen paino on väritetty vihreällä, sinisellä, punaisella tai violetilla. Onko mahdollista, että eri värein väritetyt punnukset painaisivat yhtä paljon?
Ratkaisu: Jos vastaus olisi kyllä, niin olisi
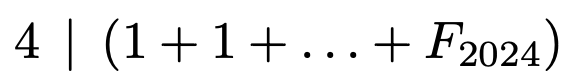
Mutta Fibonaccin luvuille pätee
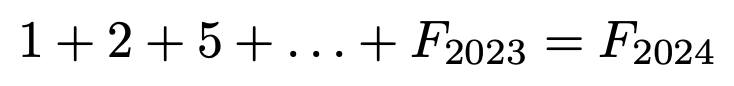
ja
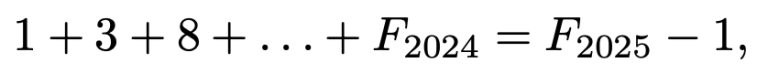
joten
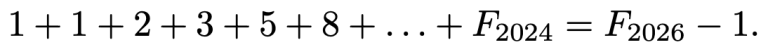
Fibonaccin lukujen jakojäännökset neljällä jaettaessa ovat 1, 1, 2, 3, 1, 0, ja nämä toistavat itseään. Siten luvun
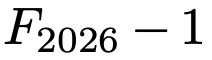
jakojäännös neljällä jaettaessa on 2, eli kyseessä ei ole neljällä jaollinen luku. Siis vastaus kysymykseen on kielteinen.
SUDOKU

DIVISIUM-3
Nyt voit pelata Divisium-3-pulmapeliä myös verkossa: www.tek.fi/fi/uutiset-blogit/ratkaise-divisium-3
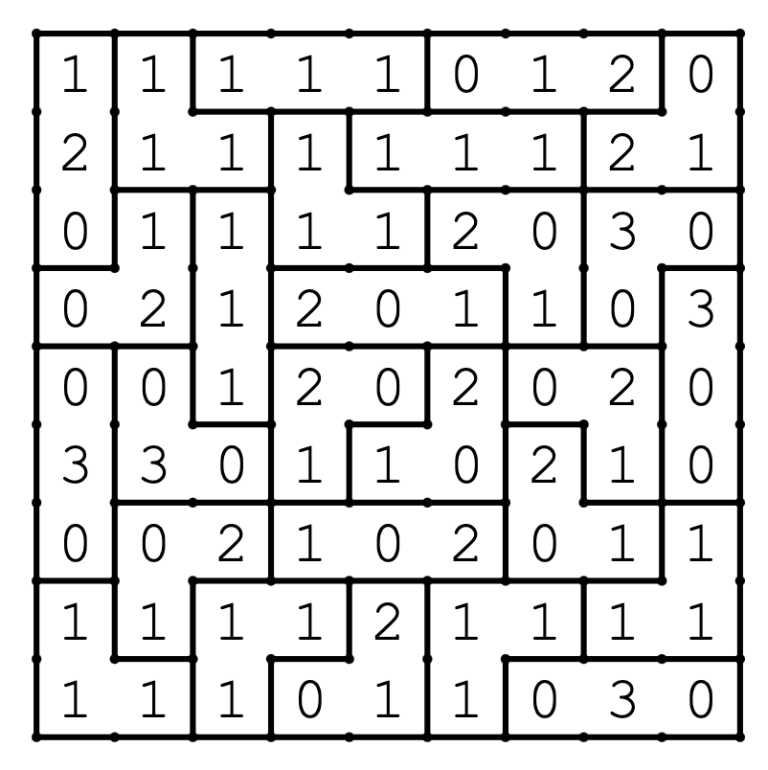

Pakopulma 1: Tehtävä alkaa oikeasta yläreunasta, jossa kehoitetaan vetämään naruista (PULL). Ainoastaan ylin solmu (4) aukeaa, joten siinä oleva pallo painaa alaolevaa vipua, joka kiertää ratasta, joka avaa vasemman puoleisen vesihanan. Vesi valuu alla olevan astiaan (X), josta oikean puoleiseen (8), siitä alempaan (X) ja siitä oikean puoleiseen (5). Vesi menee lopulta vasemman puoleiseen tankkiin (-), josta valuu yli ja alla olevaan suppiloon (3).
Suppilosta vettä valuu kaikkiin putkiloihin, joissa on eri aineita. Ainoastaan Kalium (K) reagoi voimakkaasti veden kanssa, jolloin yli siipiratas lähtee pyörimään (X), mikä vapauttaa avaimen näköisen pinnin keinulaudasta. Koska kaikki painot ovat oikealla puolella, kaatuu keinulautuu oikealle. Rauta ja Nikkeli ovat ferromagneettisia, joten ne jäävät lautaan kiinni, jolloin vain Tina(Sn) ja Kupari (Cu) tippuvat kuppiin ja nostavat mittarin kohtaan kaksi (2).
Kyseisestä reitistä muodostuu laskutoimitus 4x8x5-3x2, jossa kertolaskut lasketaan ensin, ja tulokseksi saadaan: 154.

Pakopulma 2: Käyrät ovat kolmessa ryhmässä riveittäin, joissa kussakin vasemman puoleisimmat käyrät ovat esimerkkejä, joiden perusteella tyhjät laatikot tulee täyttää. Eli kaksi ylimmäistä käyrää määrittävät aina alimpana olevan kolmannen käyrän. Kussakin käyrässä on kaksi "tilaa", "ylä" ja "ala". Kun tarkastellaan ylärivissä vasemman puoleisia käyriä (kolmea ylintä), huomataan että kun 1. ja 2. käyrä ovat molemmat alatilassa, on myös 3. käyrä alatilassa. Jos jompikumpi ylemmistä käyristä on ylätilassa, myös 3. käyrä on ylätilassa. Jos 1. ja 2. käyrä molemmat ovat ylätilassa, niin silloin 3. käyrä on alatilassa. Tällä samalla periaatteella tulee täyttää kaikki ylimmän rivin kolme laatikkoa. Tuloksena liitteessä näkyvät käyrät.
Toisessa rivisissä on miinuslasku 1.-2., jossa alin tila on alatila. Eli alatila-alatila = alatila, alatila-ylätila=alatila, ylätila-ylätila= alatila ja ylätila-alatila = ylätila.
Kolmannessa rivissä: 3. rivi on alatilassa mikäli molemmat muut ovat alatilassa, muussa tapauksessa 3. rivi on ylätilassa.
Tuloksena saadut käyrät ovat morsekoodia, joista muodostuu riveittäin kirjaimet: S I X, O N E ja T W O. Eli koodiksi tulee 612.
TEK 2/2024 -lehdessä julkaistujen Pulmien, Sudokun ja Divisium-3:n ratkaisut
Tehtävät: Anne-Maria Ernvall-Hytönen ja Esa Vesalainen, Sudoku: Arto Inkala, Divisium-3: Vesa Timonen
PULMA 1
Ongelma: Olkoon k positiivinen kokonaisluku. Onko olemassa positiivista kokonaislukua N, jolle kertoma N! päättyy
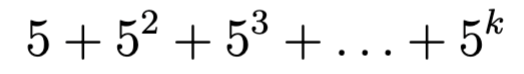
nollaan?
Ratkaisu: Kun N on positiivinen kokonaisluku, de Polignacin kaava kertoo, että kertoman N! alkutekijähajotelmassa esiintyy
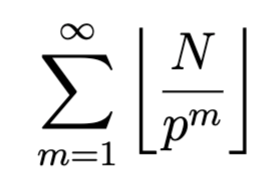
kappaletta mitä tahansa tiettyä alkulukua p. Jos luvun N! alkutekijähajotelmassa esiintyy a kappaletta alkulukua 2, ja b kappaletta alkulukua 5, niin kertoma N! päättyy luonnollisesti min{a,b} nollaan. Koska de Polignacin kaavan summa on vähenevä alkuluvun p kasvaessa, päättyy N! aina b nollaan. Toisaalta, voimme samalla todeta, että luvun N kasvaessa eksponentti b on myös kasvava.
Kertomassa
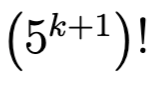
esiintyy lopussa
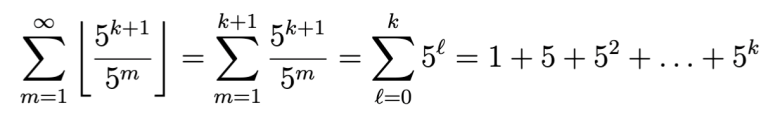
nollaa. Tämä on enemmän kuin toivottu nollien lukumäärä. Toisaalta, edellisessä kertomassa
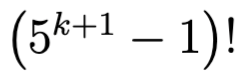
esiintyy lopussa k+1 nollaa vähemmän, eli vähemmän kuin toivottu määrä nollia. Siten millään kertomalla ei esiinny toivottua määrää loppunollia.
PULMA 2
Ongelma: Olemme löytäneet söpön ruuvikäyrän, joka koostuu pisteistä (cos2πt, sin2πt, t), missä t käy läpi kaikki reaaliluvut. Onko olemassa tasasivuista kolmiota, jonka jokainen kärki olisi ruuvikäyrällämme?
Ratkaisu: Merkitkäämme jokaiselle reaaliluvulle t P(t) = (cos2πt, sin2πt, t), ja tarkastelkaamme kolmea pistettä P(-t), P(0) ja P(t), kun t kasvaa arvosta t=0 arvoon t=1/2. Symmetrian vuoksi pisteiden P(t) ja P(0) välinen etäisyys f(t) on yhtä suuri kuin pisteiden P(-t) ja P(0) välinen etäisyys. Lisäksi f(t) muuttuu jatkuvasti, kun t kasvaa arvosta 0 arvoon 1/2. Toisaalta pisteiden P(t) ja P(-t) välinen etäisyys g(t) muuttuu niin ikään jatkuvasti, kun t kasvaa arvosta 0 arvoon 1/2. Koska P(±1/4) = (0, ±1, ±1/4), ja P(±1/2) = (-1, 0, ±1/2), on
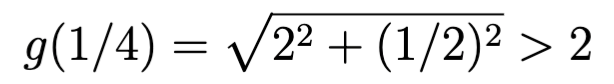
ja g(1/2)=1. Toisaalta,
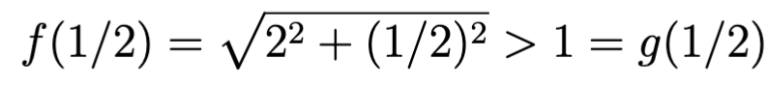
ja
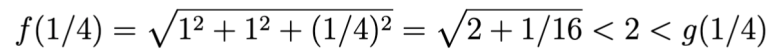
. Koska f(t) ja g(t) riippuvat jatkuvasti muuttujasta t, mutta niiden suuruusjärjestykset ovat vastakkaiset välin [1/4,1/2] päätepisteissä, täytyy olla olemassa reaaliluku t, jolle 1/4<t<1/2 ja f(t)=g(t). Tälle t ruuvikäyrämme pisteet P(-t), P(0) ja P(t) muodostavat kuin muodostavatkin tasasivuisen kolmion kärjet.
PULMA 3
Ongelma: Mikä on lukujen
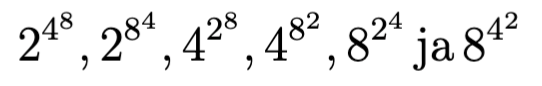
keskinäinen suuruusjärjestys?
Ratkaisu: Lukuja voi vertailla mukavasti, jos ne kirjoittaa kahden potensseina:
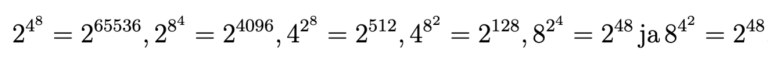
Luvut olivat jo siis valmiiksi laskevassa suuruusjärjestyksessä, missä viimeiset kaksi lukua ovat yhtä suuret.
PULMA 4
Ongelma: Tarkastellaan oheista kuviota. Lähtökohtana on neliö, jonka sivun pituus on 8. Neliön jokaisesta kulmasta on poistettu suorakulmainen kolmio, jonka kateettien pituudet ovat 1. Tämän jälkeen kärkipisteet on yhdistetty neliön keskustaan ja saadut ohuet kiilat on maalattu sinisiksi. Määritä sininen pinta-ala.
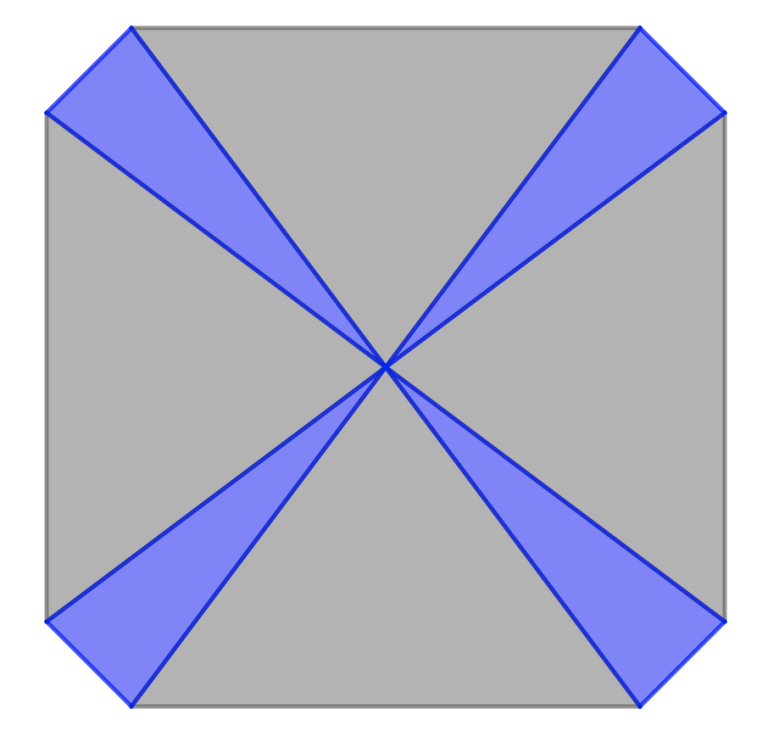
Ratkaisu: Alkuperäisen neliön pinta-ala on 64. Kulmista on poistettu yhteensä 2 yksikön verran. Kuviossa harmaana näkyvien kolmioiden kannat ovat 6 ja korkeudet 4. Niiden yhteenlaskettu ala on siis 48. Kiilojen ala on siis 64-2-48=14.
SUDOKU

DIVISIUM-3
Nyt voit pelata Divisium-3-pulmapeliä myös verkossa: www.tek.fi/fi/uutiset-blogit/ratkaise-divisium-3